Magic Numbers
Addison Wesley - Hacker’s Delight
The basic trick is to multiply by a sort of reciprocal of the divisor d, approximately
, and then to extract the leftmost 32 bits of the product. The details, however, are more complicated, particularly for certain divisors such as 7.
Let us first consider a few specific examples. These illustrate the code that will be generated by the general method. We denote registers as follows:
n - the input integer(numerator)
M - loaded with a “magic number”
t - a temporary register
q - will contain the quotient
r - will contain the remainder
Signed Divide by 3
1 | li M,0x55555556 Load magic numbers, (2**32 + 2) / 3. |
Proof. The multiply high signed operation (mulhs) cannot overflow, as the product of two 32-bit integers can always be represented in 64 bits and mulhs gives the high-order 32 bits of the 64-bit product. This is equivalent to dividing the 64-bit product by and taking the floor of the result, and this is true whether the product is positive or negative. Thus, for n $\ge$0 the above code computes
Now, , because is the largest representable positive number. Hence the “error” term is less than 1/3 (and is nonnegative), so we have .
For n<0, there is an addition of 1 to the quotient. Hence the code computes
where we have used Theorem:
For n, d integers, d>0,
If d<0:
Hence
For ,
This establishes that the quotient is correct. That the remainder is correct follows easily from the fact that the remainder must satisfy , the multiplication by 3 cannot overflow (because ), and the subtract cannot overflow because the result must be in the range -2 to +2.
The multiply immediate can be done with two add’s, or a shift and an add, if either gives an improvement in execution time.
On many present-day RISC computers, the quotient can be computed as shown above in nine or ten cycles, whereas the divide instruction might take 20 cycles or so.
Unsigned Divide by 3
For a non-power of 2, let us first consider unsigned division by 3 on a 32-bit machine. Because the dividend n can now be as large as , the multiplier is inadequate, because the error term can exceed 1/3. However, the multiplier is adequate. The code is
1 | li M,0xAAAAAAAB Load magic number, (2**33+1)/3. |
An instruction that gives the high-order 32 bits of a 64-bit unsigned product is required, which we show above as mulhu.
To see that the code is correct, observe that it computes
For , so by Theorem:
For n, d integers, , and x real,
.
In computing the remainder, the multiply immediate can overflow if we regard the operands as signed integers, but it does not overflow if we regard them and the result as unsigned. Also, the subtract cannot overflow, because the result is in the range 0 to 2, so the remainder is correct.
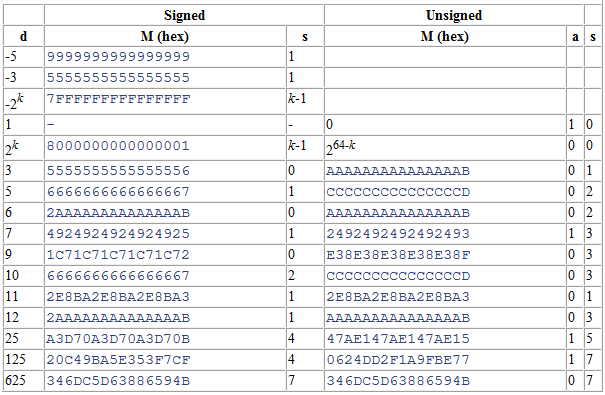
Sample Magic Numbers
Some Magic Numbers for W=32
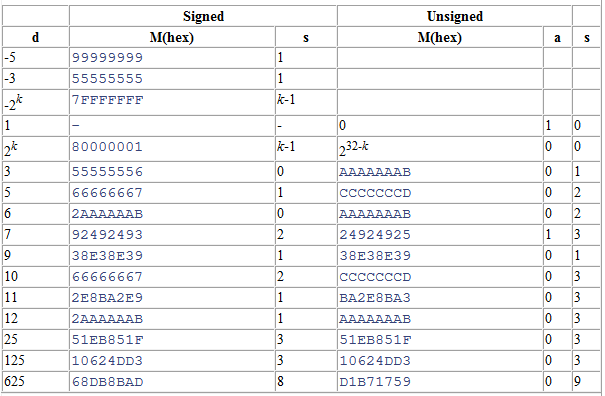
Some Magic Numbers for W = 64